Warning: Dibutuhkan pengetahuan mengenai integral dan diverensial untuk mengerti tulisan ini, tapi kalo gak ngerti integral dan deverensial anda hanya perlu percaya apa yang saya tulis benar 😉
Udah pernah saya katakan disini bahwa adalah irasional..
Nah..sekarang saya akan membuktikan bahwa irasional.
Sebenarnya ini mau saya posting kemarin tapi karna saya pembuktiannya lumayan ngejelimet saya butuh waktu tuk mempelajarinya
Ada beberapa cara /metode untuk membuktikan irasional, kali ini cara yang saya pakai adalah cara dari lambert, yang membuktukan
irasional pada tahun 1761
Diambil sebarang bilangan bulat positif dan
, didefinisikan fungsi
Bisa kita lihat bahwa jika diambil cukup besar maka akan menghasilkan nilai yang sangat kecil, boleh dibilang mendekati nol.
Dengan menggunakan teori binomial, fungsi tersebut bisa kita tulis menjadi
dengan adalah bilangan bulat.
Untuk maka
(2)
Nah sekarang akan diasumsikan rasional . misalkan
untuk
bilangan bulat positif
untuk didefinisikan fungsi
(3)
Diketahui bahwa dan
jika
atau
tapi jika maka
diketahui bahwa jika maka
mempunyai nilai yang sama, maka
dan
hasilnya adalah bilangan bulat.
Dari persamaan (3) akan ditunjukan:
Kemudian diintegralkan diperoleh
Yang merupakan bilangan bulat positit
padahal menurut (2)
Untuk cukup besar kita akan mendapatkan kontradiksi.
QED
Any question?
Credit:
Thanks, to zaki, yang membantu saya memahami pembuktian diatas


Reblogged this on Belajar Matematika.
Pingback: Okay, dia benar selanjutnya buktikan dengan Induksi « Proof { }
Masukkan:
1. Tidak ada yang salah dengan jawaban saya.
2. Luas mempunyai dimensi L^2 bukan L(untuk panjang).
3. Karena yang ada pakai dalam bentuk degree coba ganti dalam bentuk radian. Itu juga mengapa di Wolframalpha muncul 180, karena 1pi radian=180 derajat.
4. Boleh lihat disini untuk luas segitiga sama sisi http://3.bp.blogspot.com/-rvcpTXIwzpk/TiQ-gC3CKUI/AAAAAAAAABs/xP_ajMvpfAg/s1600/coba2….jpg
salah darimana?
tapi jujur saya tak mengerti darimana dan bagaimana wolframalpha bisa menjabarkan seperti itu.
Yang jelas saya sudah mem-plot persamaan tersebut kedalam grafik dan didapat pi dengan pendekatan 3.14. Bisa lihat disini http://1.bp.blogspot.com/-ni-gWBguMwc/TiJoaJR387I/AAAAAAAAABg/JDyC2a8eIgQ/s1600/Untitled.jpg
Anda mengatakan
Hukum Sinus pada sebarang segitiga berkata
karena kita berbicara segitiga sama sisi yang setiap sisinya sama dan setiap sudutnya mempunyai besar 60 derajat, diperroleh panjang sisi
Dengan rumus heron, diperoleh luas segitiga sama sisi
Jelas berbeda dengan formula luas segitiga sama sisi mu
Pertanyaan selanjutnya
Anda membuat plot nya pake sofware apa?
semua online ploting yang saya pakai berkata lain, contoh
wolframalpha
fooplot.
sebenarnya saya bukan anti pi-irasional, tapi saya hanya menampilkan atau menunjukkan kalau pi itu irasional tetapi orang yang membaca bisa mengerti.
Begini kalau saya mendefinisikan pi.
Ambil segitiga sama sama sisi, kita akan mencari luas segitiga tersebut dengan r jarak antara titik pusatnya dengan titik sudutnya. Maka didapat:
L=3*(1/2)*(r^2)*sin 120
Ambil segiempat, sama seperti diatas, cari luasnya.
L=4*(1/2)*(r^2)*sin 90
Ambil segilima
L=5*(1/2)*(r^2)*sin 72
seterusnya sampai segi-n
maka didapat:
L=(n+2)*(1/2)*(r^2)*sin {360/(n+2)}
dengan n adalah bilangan bulat positif, n>1.
Kita tau lingkaran adalah segi-oo, maka luasnya adalah:
L=pi*r^2
dengan pi:
Mohin maaf caramu mendefinsikan kurang tepat. Kamu menggunakan ide yang sama dengan Archimedes, menghitung
kurang tepat. Kamu menggunakan ide yang sama dengan Archimedes, menghitung  dengan menggunakan segi tak hingga tetapi bukan begitu caranya.
dengan menggunakan segi tak hingga tetapi bukan begitu caranya.

Lagipula
silahkan dicek dengan wolframalpha
Secara eksplisit pejelasan diatas sudah benar(walau kita tahu pi adalah perbandingan k/D bukan k/r).
Sekarang pi “telah dibuktikan adalah bilangan irasional”. Bagaimana kita dapat membuktikan(secara analisi geometri) bahwa kalau keliling rasional pastilah diameternya irasional begitu sebaliknya kalau kelilingnya irasional berarti diameternya rasional?.
Oh iya saya sala hahaha…thaks atas koreksinya sebagai rasio antara keleiling dengan diameter kita tekah merepresentasikan
sebagai rasio antara keleiling dengan diameter kita tekah merepresentasikan  secara geometri . Ingat ada banyak cara merepresentasi
secara geometri . Ingat ada banyak cara merepresentasi 
Bagaimana cara membuktikan secara analisis Geometri?
Bukankah komen saya sebelumnya telah menjawab pertanyaanmu ini, dengan merepresentasikan
misalkan kita belum tahu nilai dari pi(rasional atau irasional). lalu buat sebuah lingkaran dengan jari2 r (bilangan bulat). Misalkan kita buat lingkaran disebut dengan jangka. apakah mungkin keliling yang terukur adalah bilangan irasional? karena apabila tidak irasional berarti pi rasional? sedangkan kalau irasional, bagaimana kita dapat membuktikannya?(kalau kelilingnya irasional)
Diketahui dengan
dengan 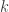 adalah keliling lingkaran dan
adalah keliling lingkaran dan 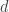 adalah diameter, telah dibuktikan bahwa
adalah diameter, telah dibuktikan bahwa  irasional
irasional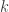 dan
dan 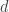 ?
?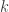 dan
dan 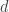 mustahil keduanya adalah bil irasional, pastilah salah-satu (atau bisa kedua-duanya) dari mereka adalah bil irasional
mustahil keduanya adalah bil irasional, pastilah salah-satu (atau bisa kedua-duanya) dari mereka adalah bil irasional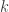 dan
dan 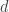 keduanya adalah bil rasional, misalkan
keduanya adalah bil rasional, misalkan  dan
dan  diperoleh
diperoleh
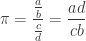
Nah…pertanyaannya
apa akibatnya terhadap
Akibatnya, pasangan
Mengapa?
Andaikan
merupakan bilangan rasional. Kontradiksi
Itu berarti Jika diketahui diameter sualu lingkaran adalah bil rasional pastilah kelilingnya adalah bil irasional, begitupula sebaliknya jika diketahui kelilingnya rasional pastilah diameternya adalah irasional
menurut saya pi adalah bilangan rasional, karena pi didapat(dulu pada saat pi pertama kali ditemukan) dari perbandingan antara keliling lingkaran dan diameternya ini berarti pi dapat dibuat dalam bentuk a/b ini jelas kontrakdiksi dengan pernyataan bilangan irasional yang tidak dapat dibuat dalam bentuk a/b.
Bilangan rasional berbentu a/b dengan sayarat a dan b nya adalah bilangan bulat. Apakah pasangan keliling dan diameter pada lingkaran keduanya adalah bilangan bulat?
mas mgapa akar3 bilangan irasional tolong buktikan ????
silahkan anda baca
http://www.grc.nasa.gov/WWW/k-12/Numbers/Math/Mathematical_Thinking/irrationality_of_3.htm
Mas aku pernah baca sekilas (sekilas ,lho) “Ramanujan Notebook” seperti ini. Misal luas lingkaran= persegi a. Maka
pi.r^2 = a^2
pi= a^2/r^2, berarti pi rasional. Maksudnya gi mana ini?
Itu maksudnya apa? itu tidak membuktikan apa apa
lo pi dikonversikan ke biner tw bil. basis lain miasal 8 gmn???????????
Mohon maaf saya kurang tahu
Bilangan basis 2 dan 8 kan cuma bentuk lain bilangan bulat, sedangkan pi bukan bil.bulat.
@watchmath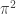 rasional tetapi kita malah memperoleh
rasional tetapi kita malah memperoleh 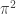 irasional artinya asumsi kita salah karena
irasional artinya asumsi kita salah karena 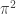 irasional maka
irasional maka  juga irsional
juga irsional bulat?
bulat?
Itu hanya asumsi aja, kita asumsikan
Kenapa
coba baca lagi postingan diatas, disitu saya mengatakan
maka kita peroleh

bagaimana sudah jelas?
Pernyataan jika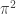 rasional maka
rasional maka  rasional tidak tepat. (contohnya untuk
rasional tidak tepat. (contohnya untuk  , pernyataan jika
, pernyataan jika 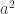 rasional maka
rasional maka  rational adalah pernyataan yang salah). Harusnya jika
rational adalah pernyataan yang salah). Harusnya jika 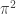 irasional maka
irasional maka  irasional.
irasional. bulat? mohon penjelasannya…
bulat? mohon penjelasannya…
Mengapa
Cm adalah koefisien dari x^m, Cm=2nCm.
kalo belum ngerti juga, tolong pelajari teorema binomial
iy… tapi kalo kombinasi selalu ada 2 unsur
Misalnya 3C2 = 3 atau 4C2 = (4!)/(2!2!) = 6…
Nah, kalau C_m di sini maksudnya apa?
Itu yang mau saya tanya.
Thx
Cm itru kombinasi, kamu ngerti teorema binomial gak? coba kamu pelajari itu dulu?
Hebat. bIsa postingan materi tahap dewa… Aku mo nanya.
Jika c_m itu bilangan bulat, maksudnya:
c_n itu berapa? c_{n+1} itu berapa? c_{n+2} itu berapa? dan seterusnya? Itu bagian yang membuat saya bingung… =.=”
Thx very much ^^