Sory nich baru sempet update blog lagi, soalnya saya lagi sibuk skripsi. Kali ini saya pangen ngomongin mengenai “pembuktian”, blog ini bernama “proof (pembuktian)” tapi apakah kalian tahu apa itu “pembuktian” dalam matematika?
***
Di Sekolah kita diajarlan bagaimana memghitung luas lingkaran, menemukan solusi dari suatu persamaan, mencari nilai minimum suatu fungsi, okey matematika memang bisa melakukan itu tetapi Matematika bukanlah mengenai hal tersebut. Matematika adalalah Ilmu yang mempelajari hukum dibalik bilangan, aljabar, dan Geometri. Bagaimana menemukan hal yang baru dari suatu sistem, memperluas system yang ada, menjelaskan hubungan 2 buah objek, menjelas fenomena baru yang kita temukan, itulah matematika, bahkan dengan matematika kita bisa menciptakan sistem baru dengan menggunakan sistem yang sudah ada.
Matematika dan pembuktian
Di dalam matematika, jika kita berkata dua buah objek A dan B memepunyai hubungan/keterkaitan maka satu-satunya cara supaya orang percaya apa yang kita katakan adalah dengan membuktikannya. Di matematika semua pernyataan/statement baik yang paling sulita maupun yang paling mudah membutuhkan pembuktian valid agar pernyatan tersebut diakui (pernyatan yang telah dibuktikan disebut teorema), inilah yang memebedakan Matematika dengan ilmu lainnya di TV kita sering melihat para tokoh mengeluarkan pernyataan politis tanpa ada pembuktiannya. Selama saya belajar matematika, saya menyimpulkan bahwa matematika “hanyalah” kumpulan pernyataan beserta pembuktiannya yang terkumpul dalam wadah besar bernama logika. Lau sekarang apa itu pembuktian?
Pembuktian adalah langkah-langkah logis untuk menunjukkan atau meyakinkan orang lain bahwa suatu pernyataan matematis itu benar ( untuk menunjukan suatu pernyataan adalah salah cukup dicari counter example nya)
***
Pada 2300 tahun yang lalu Euclid berkata
Teorema Euclid: ada tak hingga banyaknya bilangan prima
sampai detik ini kita tidak tahu bagaimana mencari bilangan prima, yang bisa kita lakukan adalah mencek suatu bilangan apakah prima atau bukan.Pada tahun 2008 kemarin ditemukan bilangan prima dengan digit terbesar sebanyak 13 juta digit, Meskipun begitu Matematikawan yakin bahwa ada bilangan prima dengan digit sebanyak 15 juta digit bahkan 20 juta digit sekalipun. Kenapa? Karena matematikawan yakin apa yang dikatakann Euler? Kenapa yakin? karna Euler mampu membuktikan apa yang dikatakannya
Bukti Teorema Euler: Akan dibuktikan dengan kontradiksi, andaikan bilangan prima itu terbatas maka terbentuk himpunan yang berisikan semua bilangan prima. Diperoleh bilangan
hasil dari perkalian semua bilangan prima maka jelas
tidak memepunayai faktor di
padahal menurut teorema fundamental aritmatika semua bilangan bulat positif yang lebih besar dari satu mempunyai faktor bilangan prima. Jadi jika bilangan prima terbatas maka akan kontradiksi dengan teorema fundamental. Bukti komplit
***
Banyak orang awam berpendapat orang yang jago matematika, orang yang hebat matematika nya adalah orang yang menghitung dengan cepat, yang bisa menghitung 3456745×9757856 tanpa menggunakan kalkulator tapi sebenarnya bukan itu pengertian “jago”,”hebat” dalam matematika, seorang matematikawan dikatakan jago, dikatakan hebat jika dia bisa membuat suatu pernyataan yang baru, yang orisinil dan membuktikannya secara valid. Membuat pernyataan dan sekaligus membuktikannya bukanlah hal yang mudah. Bahkan seorang Dewa Matematika, Riemann sekalipun tidak sanggup membukttikan pernyataannya sendiri, yang dikenal dengan Hipotesis Riemann
Isi dari pembuktian
Nah..sekarang kita lihat apa isi dari pembuktian teorema Euclid, bisa kita lihat untuk membuktikan teorema Euclid diperlukan teorema Fundamental Aritmatika. Jadi pada umumnya untuk membuktikan suatu teorema digunakan teorema lain yang telah terbukti atau dengan kata lain dari teorema yang ada dapat diperoleh/diturunkan teorema yang baru, dari teorema fundamental aritmatika diperoleh teorema Eucli, dari teorema A diperoleh teorema B, dari teorema B diperoleh teorema C dan seterusnya, dengan cara seperti inilah matematika berkembang. Nah..jika suatu teorema berasal dari teeorema lainnya muncul pertanyaan dimana pangkalnya, dimana pangkalnya, dimana titik mulainya?
Matematika berpangkal dari aksioma atau postulat (Aksioma dan postulate mempunyai pengertian yang sama)
Apa itu aksioma?
Aksioma itu adalah fakta-fakta fundamental dari matematika yang diyakini kebenarannya tanpa perlu dibuktikan. Aksioma merupakan Iman di matematika. Dari aksioma lah para matematikawan bergerak, mengekplorasi hal-hal baru. Pembuktian teorema Euclid diatas menngunakan aksioma Peano yang mengatakan
Nah..ada satu hal mendasar untuk bisa memebuktikan teerema Euclid, kita harus tahu definisi dari bilangan Prima.
Apa itu definisi?
Definisi adalah istilah teknis atau terminologi dalam matematiaka. Definisi haruslah bersifat universal dan tidak ambigu. Definis bilangan prima di Indonesia haruslah sama dengan definisi bilangan prima di Timbukthu
***
Sekarang bisa kita simpulkan bahwa pembuktian pada umumnya berisi tiga hal
- Teorema lain
- Akioma
- Definisi
Saya tegaskan pada umumnya karna belum tentu suatu pembuktian mengandung tiga hal tersebut tergantung kebutuhan. Jadi untuk memebuktikan suatu pernyataan kita harus mencari teorema lain, aksioma dan definisi yang diperlukan, lalu rangkai semua berdasarkan kaida-kaidah logika akhirnya pembuktian siap dihidangkan 🙂
Abadi, tak akan pernah berubah
Dahulu kala para Fisikawan berpendapat bahwa kecepatan benda jatuh tergantung dari massanya semakin berat massa nya, maka semakincepat jatuhnya tapi Galileo membuktikan bahwa kecepatan benda jatuh tidak tergantung dari massanya tapi tergantung dari Gravitasi dan gaya gesek benda tersebut terhadap udara. Hal ini tidak akan terjadi pada matematik, seperti yang saya bilang pernyatan matematika tidak diperoleh melalui data-data emperik yang terkadang salah. Para Ilmuwan (Non-matemtikawan) umumnya menngunakan suatu metode mengeksplore hal baru, kemudian hal baru (kalau mereka dapat) tersebut di uji dengan suatu metode pengujian di laboratorium atau ditempat lainnya tetapi matematikawan tidak bekerja seperti itu untuk mengeksplore hal baru, untuk mengeksplore hal baru, matematikawan mengumpulkan aksioma, definisi serta teorema yang dibutuhkan kemudian merangkainya menurut kaidah logika untuk memperoleh hal baru, jadi sbenernya hal baru jadi hal baru dari matematika merupakan rangkaian baru dari fakta-fakta kebeneran matematis yang telah ada (baca: aksioma) kemudian hal baru tersebut dibuktikan, jika hal baru tersebut dapat dibuktikan secara valid maka hal baru tersebut akan menjadi fakta matematika. Jadi pembuktian merupakan final test bagi semua hal baru di Matematika. Jadi pembuktian membuat orang percaya, yakin mengenai suatu hal di matematika. serta dengan pembuktian valid membuat orang mustahil menemukan counter example dari hal tersebut.
Itulah sebanbya teoreama Euclid dan teorema Pythagoras yang telah dibuktikan 2500 tahun lalu tidak akan pernah berubah sampai hari kiamat sekalipun.


bagaimana membuktikan 1+1=2?
silahkan buk ahttps://ariaturns.com/2008/09/11/pembuktian-112/
artikelnya menarik…thanks
Artikel dan blog menarik, trims
saya pnya soal ttng pembuktian.
S={1/n , n€N}
Buktikan sup S = 1?
Mohon bantuannya ya pak….
Clue: Ambil sebarang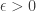 tujukan terdapat
tujukan terdapat 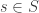 sedemikian hingga
sedemikian hingga 
mas mnt tolong dung sertakan file tentang 48 dalil euclides dari buku 1 the elements
Makasih mas, benar2 membuka wacana ane yang lagi belajar matematika 😀
boleh jelasin pengertian dalil,teorema,postulat,aksioma dan lemma gak???? penting x ni 🙂
thx 🙂
om..
bisa jelasin gak tentang kurva agnesi???/
tolong yah..
Coba aja baca di planet math
http://planetmath.org/encyclopedia/WitchOfAgnesi.html
udah cukup jelas
Betul, Matematika Adalah Ilmu Eksak yg kebenaranna tidak akan berubah sepanjang masa…
luar biasa…
saya sangat terbantu, terlebih lagi karena sudah lama tidak bergelut dengan matematika…
Mas Aria, saya amati bahwa matematikawan cenderung sangat berhati-hati dalam hal diksi. Untuk bisa mengatakan “Aksioma merupakan Iman di matematika”, ada syarat yang harus dipenuhi, yakni kata “Iman” itu sendiri mesti anda definisikan terlebih dahulu. Bagaimana?
-Fraleigh, the author of A First Course in Abstract Algebra–
Jadi dalam dunia matematika sekalipun mustahil menjelaskan semua hal secara jelas
Mas Aria bisa bantu saya bagaimana membuktikan kaidah euler dengan menggunakan tabel?
ooo.. thanks