
Lemma Zassenhaus: Diberikan grup dengan
dan
maka berlaku:
Lemma Zassenhaus sering disebut lemma Kupu-kupu, karena jika digambarkan dalam bentuk diagram akan menyerupai kupu-kupu
Bagaimana mirip kupu-kupu, tidak? Jujur, menurut saya tidak 🙂 . Pada diagram diatas, ujung bawah garis adalah subgrup dari ujung atasnya. Sedangkan garis-garis biru menunjukan ujung bawah merupakan subgrup normal dari ujung atasnya dan juga isomorfisma:
Dari diagram diatas, bisa kita lihat bahwa isomorfisma tersebut simetris dalam artian sisi kanan diperoleh dari sisi kiri dengan menukar simbol dengan
.
Bukti:
Karena maka untuk menunjukan
cukup menunjukkan
. Untuk menunjukkannya, kita harus menunjukkan: jika
dan
maka
. Diketahui
maka
dengan
dan
tapi juga
karena
. Dengan cara yang sama kita menunjukkan
.
Oleh karena dan
merupakan subgrup normal maka jelas
karena dibangun dari 2 subgrup normal
Selanjutnya akan ditunjukan
.
Karena simetri maka cukup ditunjukkan .
Diberikan pemetaan
dengan , didefiniskan
dengan
dan
. Selanjutnya akan ditinjukan Pemetaan
well-defined dan homomorfisma.
Diberikan dan
. Jika
maka
Jadi , terbukti
well-defined.
Karena normal didalam
, maka terdapat
sedemikian hingga
, diperoleh:
Terbukti homomorfisma.
Jelas surjektif. Terakhir, jika
dan
maka
. Itu berarti
, atau dengan kata lain
.
Itu berarti . Dengan menggunakan Teorema isomorfisma pertama diperoleh
.
QED
Boleh dibilang Lemma Zassenhaus merupakan generalisasi dari teorema isomorfisma kedua.
Notasi
:
subgrup dari
:
subgrup normal dari
:
dan
isomorphic



ka’ mau nanya donk..
knapa untuk mmbuktikan A1(AnB1) subgrup normal dari A1(AnB) cukup dngan mmbuktikan (AnB1) subgrup normal dari (AnB)?
mohon pnjlasan lbih lanjut. 🙂
Karena , Nah..sekarang pertanyaannya:
, Nah..sekarang pertanyaannya: maka untuk membuktikan
maka untuk membuktikan 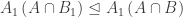 cukup membuktikan
cukup membuktikan 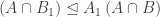 ? Silahkan anda jawab sendiri 🙂
? Silahkan anda jawab sendiri 🙂
Mengapa jika diketahui
ka’……… grup koesen itu sama g’ sma grup faktor ?
Yup.. sama